인터넷에서 어그로를 열심히 끌던 다음 문제를 기억하는 사람이 있을 것이다.

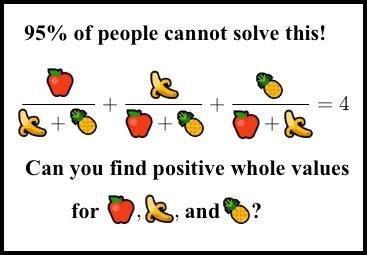
95% of people can't solve this!

국내 인터넷에는 MIT 졸업생 95%가 못 푸는 문제라는 이름으로 돌아다니는 것 같다. 나무위키에도 잘 설명이 되어 있듯이, 이 문제는 전형적인 디오판토스 문제이다.

다행히도, 이 문제는 Bremmer와 Macleod에 의해 이미 연구되어서, 우리까지 머리를 싸매고 고민할 필요는 없다. 둘의 논문은 여기에서 확인할 수 있다. 심심해서 이 논문을 구현한 코드를 직접 짜 보았다. N=4N = 4뿐만 아니라 다른 경우에 대해서도 해를 찾을 수 있다. 실행에는 SageMath가 필요하다.

from sage.all import *

"""
Solve a/(b+c) + b/(a+c) + c/(a+b) = N
Reference: https://ami.uni-eszterhazy.hu/uploads/papers/finalpdf/AMI_43_from29to41.pdf
"""

N = 6  # Fun fact: There is no solution when N is odd!

print(f"[+] Finding solution for: a/(b+c) + b/(a+c) + c/(a+b) = {N}")

# Build an elliptic curve and mapping.
E = EllipticCurve([0, 4 * N**2 + 12 * N - 3, 0, 32 * (N + 3), 0])
T = [E(t) for t in E.torsion_subgroup()]

print(f"[+] Elliptic curve: {latex(E)}")


def point_to_sol(x, y):
    a = 8 * (N + 3) - x + y
    b = 8 * (N + 3) - x - y
    c = 2 * (-4 * (N + 3) - x * (N + 2))

    if a < 0:
        a, b, c = -a, -b, -c

    g = GCD(GCD(a, b), c)

    return a // g, b // g, c // g


# Get one integral point of E.
P = E.integral_points()
# Generator must be inside the "egg".
for p in P:
    if p[0] < 0:
        break
print(f"[+] Found integral point: {p}")
cnt = 1
q = p

# Iterate until we find positive solution.
is_found = False
while True:
    print(f"[*] Trying {cnt} * P")

    for qq in [q] + [q + t for t in T]:
        a, b, c = point_to_sol(qq[0], qq[1])

        if (a > 0) and (b > 0) and (c > 0):
            print("[+] Found a, b, c!")
            is_found = True
            break

    if is_found:
        break

    q += p
    cnt += 1

print(f"[+] a = {a}")
print(f"[+] b = {b}")
print(f"[+] c = {c}")

# Check!
assert a / (b + c) + b / (c + a) + c / (b + a) == N

(GitHub Gist)

이제 당신도 상위 5% 수잘알이 되었다!!

자세한 설명은 역시 나보다는 논문을 참고하는 것이 더 좋을 것 같다. 핵심적인 관찰은, 주어진 방정식은 다음과 같은 (Q\mathbb Q 위의) 타원 곡선으로 변형할 수 있다는 것이다.

y2=x3+(4N2+12N−3)x2+32(N+3)xy^2 = x^3 + (4N^2+12N-3)x^2 + 32(N+3)x

여기에서 mapping은 다음과 같은 꼴이다. 사실 이건 적당히 nn배를 취한 것이긴 한데, 어차피 이 방정식의 해는 상수배를 취해도 여전히 해가 되므로 큰 상관은 없다.

a=8(N+3)−x+yb=8(N+3)−x−yc=−8(N+3)−2(N+2)x\begin{align*} a &= 8(N +3)−x+y \\ b &= 8(N +3)−x−y \\ c &= −8(N +3)−2(N +2)x \end{align*}

따라서, 먼저 방정식을 타원 곡선으로 옮긴 뒤, 그 곡선의 적당한 generator를 잡고, 다시 위의 map을 이용해서 되돌려 보내면 되는 것이다.

일단 위의 코드는 주어진 식을 변형하여 만들어진 타원 곡선 EN(Q)E_N(\mathbb Q)의 rank가 1인 경우만 확실하게 풀 수 있다. 그 외의 경우에는 더 많은 generator들을 고려해야 할 것 같은데, 확실하진 않다. 이건 나중에 추가하던지 해야겠다. 어차피 이런 케이스는 개인용 컴퓨터로 충분히 빠르게 찾을 수 있을지도 잘 모르겠다.

참고로, 모든 NN에 대해서 양수 해가 존재하는 것은 아니다. 양수 해가 존재하려면,EN(Q)E_N(\mathbb Q)의 generator가 곡선의 “달걀” 부분에 있어야 한다. NN이 홀수라면 이 조건을 항상 만족하지 못하고, 짝수여도 항상 만족하는 것은 아니다. 그렇지만 이 조건을 만족하는 짝수는 무한히 많다.

Reference